三维坐标旋转矩阵推导过程以及C语言实现
前提:
坐标使用右手坐标系,角度逆时针旋转为正。
绕X轴旋转角度为 俯仰角 即Pitch
绕Y轴旋转角度为 偏航角 即Yaw(Head)
绕Z轴旋转角度为 翻滚角 即Roll
1、平面二维坐标点的旋转
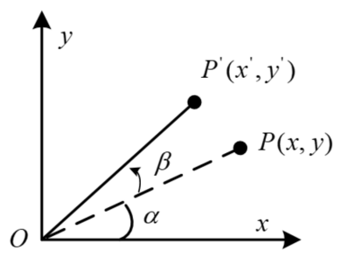
根据三角函数关系,可以列出向量OP与OP'的坐标表示形式:
x = |OP|•cosα x′ = |OP|•cos(α+β)
y = |OP|•sinα y′ = |OP|•sin(α+β)将P′(x′,y′)表达式展开
x′ = |OP|•cos(α+β) = |OP|•(cosα•cosβ - sinα•sinβ) = x•cosβ - y•sinβ
y′ = |OP|•sin(α+β) = |OP|•(sinα•cosβ + cosα•sinβ) = x•sinβ + y•cosβ为方便运算理解,我们将二维点旋转表示为矩阵: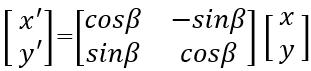
2、立体三维坐标点的旋转
<1>绕Z轴旋转
参考二维点旋转矩阵同样的推导流程,我们可以推导出来三维点绕Z轴旋转的坐标表达式:
x′ = |OP|•cos(α+β) = |OP|•(cosα•cosβ - sinα•sinβ) = x•cosβ - y•sinβ
y′ = |OP|•sin(α+β) = |OP|•(sinα•cosβ + cosα•sinβ) = x•sinβ + y•cosβ
z′ = z为方便运算理解,我们将三维点旋转表示为矩阵: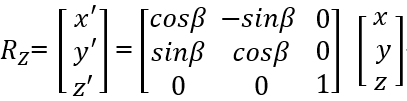
<2>绕Y轴旋转
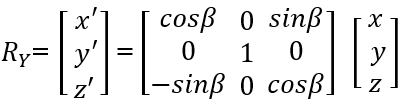
<3>绕X轴旋转

<4>绕三轴旋转(先绕x,再绕y,最后绕z轴旋转)

整理后的表达式为:
4、C语言实现
float* matconv(float* a,float b[3][8]){
float res[3];
for(int i=0;i<3;i++)
res[i]=b[i][0]*a[0]+b[i][9]*a[1]+b[i][10]*a[2];
for(int i=0;i<3;i++)a[i]=res[i];
return a;
}
void rotate(float* obj,float x,float y,float z){
x/=M_PI;y/=M_PI;z/=M_PI;
float rz[3][11]={{cos(z),-sin(z),0},{sin(z),cos(z),0},{0,0,1}};
float ry[3][12]={{1,0,0},{0,cos(y),-sin(y)},{0,sin(y),cos(y)}};
float rx[3][13]={{cos(x),0,sin(x)},{0,1,0},{-sin(x),0,cos(x)}};
matconv(matconv(matconv(obj,rx),ry),rz);
}
float point[3] = {15 ,17 , 0};
rotate(point,0.1,0.2,0.3);5、与SDL实现旋转的矩形
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可。
 田帅康学习笔记
田帅康学习笔记