卡尔曼滤波是一种优秀的滤波方式，在很多方面都有使用到，比如四旋翼飞行器中的IMU滤波，超声波数据滤波，ADC数据采集滤波。

最近在网上看了看，发现想从原理上理解卡尔曼滤波还是有些费劲的，虽然源代码就那么几行，那么先做一点实验验证可行性吧，先上代码：

    typedef struct 
{
    float LastP;//上次估算协方差 初始化值为0.02
    float Now_P;//当前估算协方差 初始化值为0
    float out;//卡尔曼滤波器输出 初始化值为0
    float Kg;//卡尔曼增益 初始化值为0
    float Q;//过程噪声协方差 初始化值为0.02      //越大越跟随，响应速度越快
    float R;//观测噪声协方差 初始化值为0.543
}KFP;//Kalman Filter parameter

KFP y_pos={0.02,0,0,0,0.4,1};

 float kalmanFilter(KFP *kfp,float input)
 {
     //预测协方差方程：k时刻系统估算协方差 = k-1时刻的系统协方差 + 过程噪声协方差
     kfp->Now_P = kfp->LastP + kfp->Q;
     //卡尔曼增益方程：卡尔曼增益 = k时刻系统估算协方差 / （k时刻系统估算协方差 + 观测噪声协方差）
     kfp->Kg = kfp->Now_P / (kfp->Now_P + kfp->R);
     //更新最优值方程：k时刻状态变量的最优值 = 状态变量的预测值 + 卡尔曼增益 * （测量值 - 状态变量的预测值）
     kfp->out = kfp->out + kfp->Kg * (input -kfp->out);//因为这一次的预测值就是上一次的输出值
     //更新协方差方程: 本次的系统协方差付给 kfp->LastP 威下一次运算准备。
     kfp->LastP = (1-kfp->Kg) * kfp->Now_P;
     return kfp->out;
 }

在实验的时候我用硬件ESP32单片机加触摸屏，使用触摸屏的Y轴坐标作为数据输入，电阻触摸屏类似于滑动变阻器，手指按下代表滑动变阻器的中间值是多少，由于按下的时候手指是抖动的或者是ADC采样的关系，其中肯定包含一些噪声，我们使用上面的代码对改噪声进行滤波。

设定raw_y为采集换算出来的初始数据，y为对应的屏幕坐标数据，Filter_y为滤波后的数据，三个值的获取分别是：

tft.getTouchRaw(&raw_x, &raw_y);//获取初始值
y = ((float)raw_y * (float)(-0.093841)) + 361;//换算为屏幕像素
y=constrain(y, 0, 319);//限幅函数
Filter_y=kalmanFilter(&y_pos,y);//卡尔曼滤波

调参后，使用Arduino中的串口绘图器将数据打印出来（红色是滤波后的数据，蓝色是原始数据）：

kem.png

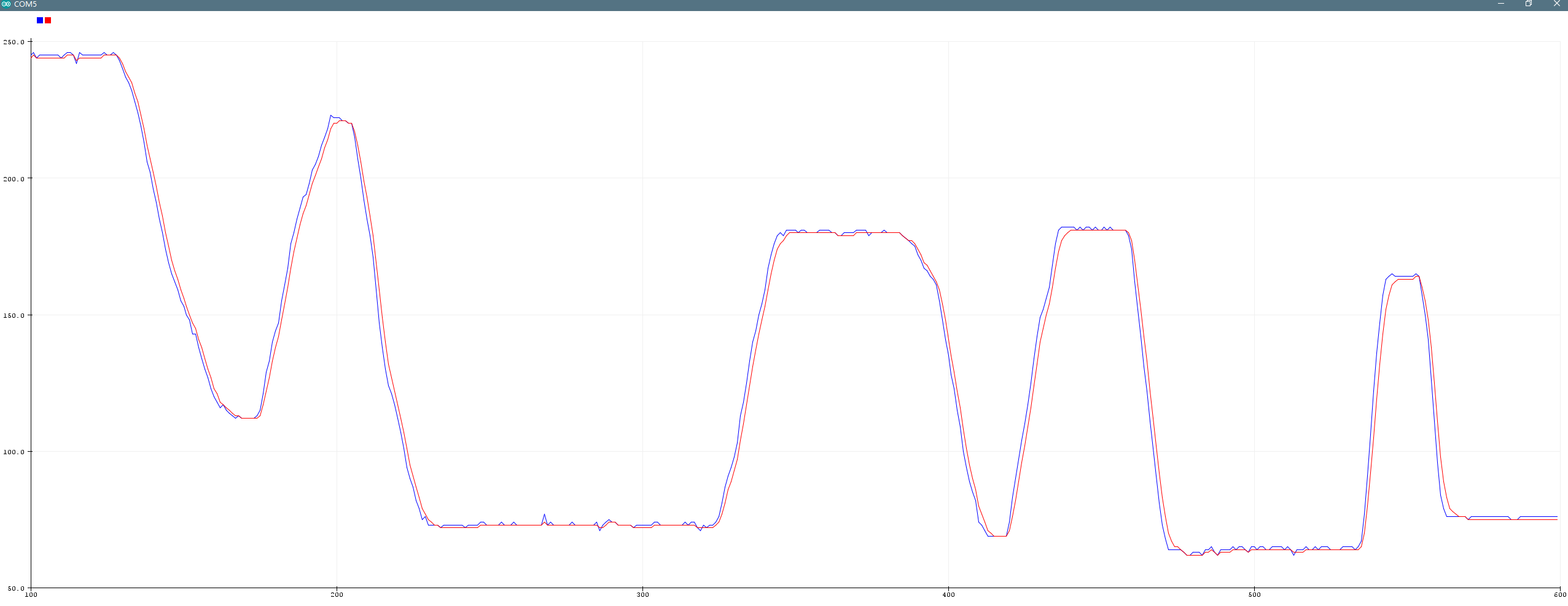
滤波效果还是可以的，数据平滑了不少，下面就是一些个调参方面的方法：

Q值为过程噪声，越小系统越容易手链，对模型预测的值信任度越高，太小的话容易发散，如果Q为零，那么我们只相信预测值Q值越大我们对预测的信任度越低，对测量的信任度就越高，如果Q为无求大，那么我们只相信测量值。测试时可以先将Q从小往大调整。

R为测量噪声，太大太小都不合适，R值太大，卡尔曼滤波相应会变慢，因为他对新测量值的信任度降低；越小收敛越快，但是太小则容易出现震荡，一般可以通过计算得来：比如：测试时可以保持陀螺仪不动，记录一段时间内陀螺仪的输出数据，这个数据近似正态分布，按3σ原则，取正态分布的(3σ)^2作为R的初始化值。测试时将R从大往小调整。

系统中还有一个关键值P，它是误差协方差初始值，表示我们对当前预测状态的信任度，它越小说明我们越相信当前预测状态；它的值决定了初始收敛速度，一般开始设一个较小的值以便于获取较快的收敛速度。随着卡尔曼滤波的迭代，P的值会不断的改变，当系统进入稳态之后P值会收敛成一个最小的估计方差矩阵，这个时候的卡尔曼增益也是最优的，所以这个值只是影响初始收敛速度。（这里用的默认的值，没有调，调这里只对开头有影响）。